今日は曇りで外出する気が薄れてしまったので、引きこもっているため書くことがほとんどありません。また最近は体脂肪率が20%を超えてしまい、減量を意識しているのでパスタも作っていないのでネタが全然ありませんし、悲しいことに思いつきもしませんでした。
92について検索してみた
今日でこの駄散文を書き始めて92日目なので、F91みたいになにかネタが見つかるかもしれないと思い、とりあえず「92」で検索してみました。そうしたらなんと、Wikipediaに92の項目がありました。
92(九十二、きゅうじゅうに、ここのそじあまりふたつ)は自然数、また整数において、91の次で93の前の数である。
「ここのそじあまりふたつ」が文字数を稼いでくれているので、最高に素敵です。
性質の項目にある五角数という単語を初めて見たので、リンクを見てみました。

五角数(ごかくすう、pentagonal number)とは、多角数の一種で、正五角形の形に点を図のように並べたとき、図に含まれる点の総数にあたる自然数である。五角数は無数にあり、そのなかでは 1 が最も小さい。3で割ると1余る整数を1から小さい順に足した数と定義してもよい。例:5 (= 1 + 4)、12 (= 1 + 4 + 7)、92 (= 1 + 4 + 7 + 10 + 13 + 16 + 19 + 22)
図も抜粋。

多角数の一種ということで、多角数も見てみます。
任意の自然数は、高々 p 個の p 角数の和で表せる。これを多角数定理という。
性質でほうほうと思いましたが、「高々」ってなんだろうと思ってまたジャンプ。
数学において、高々(たかだか)という表現は、英語の at most に対応した厳密な意味を持つ学術用語である。 「多くとも」、「以下」と同義であるが、文脈によってはこれらよりも好まれる場合もある(例:「高々可算」とは言うが「可算以下」とは言わない。)
へえええええ!上の説明に書かれていない言葉で表現すると「最大」のような意味なんですね。
92は変形十二面体の面の総数とあるので、またリンクをたどってみます。

変形十二面体(へんけいじゅうにめんたい、英: snub dodecahedron、ねじれ十二面体)または変形二十・十二面体(へんけいにじゅうじゅうにめんたい、英: snub icosidodecahedron)とは、半正多面体の一種であり、正十二面体の面をねじり、間に正三角形を入れたような立体である。キラルであり、ねじる方向により違いが現れる。正二十面体の面をねじる事によっても同じ図形を作ることができる。
半多面体のページが面白かったので読んじゃいました。半多面体は全部で13種類あって、下のページにすべての図があり、自由回転はマウスでグリグリ動かすことができます。
キラルも知らなかったので飛んでみました。
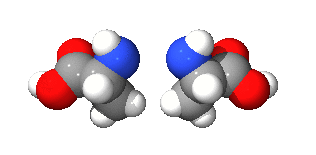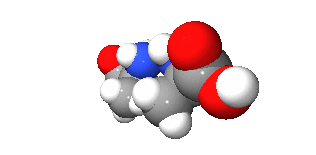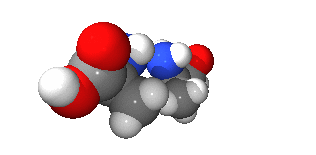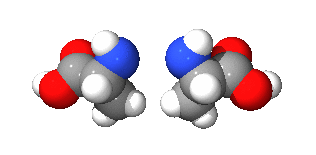
キラリティがあることをキラル (chiral) という。英語風の発音でカイラリティ、カイラルともいう。これらの語はギリシャ語で「手」を意味するχειρ (cheir) が語源である。手はキラルなものの一例で、右手とその鏡像である左手は互いに重ね合わせられない(右手の掌と左手の甲を向かい合わせたときに重なり合わないということである)。
一方でキラリティがない、つまり鏡像と重ね合わせられることをアキラル (achiral) という。キラルな図形とその鏡像を互いに(たとえば右手に対する左手を)エナンチオモルフ (enantiomorphs) と言い、ギリシャ語で「反対」を意味するεναντιος (enantios) が語源である。
対掌性(たいしょうせい)ともいう。対掌とは右と左の手のひらの対を意味している。対称性と紛らわしいが、キラリティとは鏡像対称性の欠如であり、むしろ逆の意味になる。
なんとなくわかったようなわからないような感じですが、右手と左手のように鏡像同士が重なり合わない性質をキラリティと言うみたいですね。
苦し紛れに検索してみましたが、知らないことばかりでどんどんリンクをたどってみたら結構面白かったので得をした気分です。ほとんど引用とリンクばかりのチートとも言える記事ですが、内容が今までで一番興味深い気がするのが悔しいところです。



コメント